为促进高校之间优秀老员工的交流和互动、给员工提供一个了解数学和统计学科各个方向最新前沿动态的机会,mk体育官网拟定于2023年1月7日—1月12日举办优秀老员工数学国际冬令营。本次冬令营计划在全国高校范围内招收100名数学、统计学及相关专业的高年级本科生,通过Zoom视频在线进行集中交流。
我们邀请到以下国内外专家为员工讲授专题课、作前沿报告:
周向宇 院士 中国科学院
姜铁锋 教授 美国明尼苏达大学
蒋云峰 教授 美国堪萨斯大学
孙澎涛 教授 美国内华达大学
田天海 教授 澳大利亚莫纳什大学
徐小文 研究员 北京应用物理与计算数学研究所
崔 涛 研究员 中国科学院
许现民 研究员 中国科学院
刘民千 教授 南开大学
陈良云 教授 东北师范大学
周海港 教授 同济大学
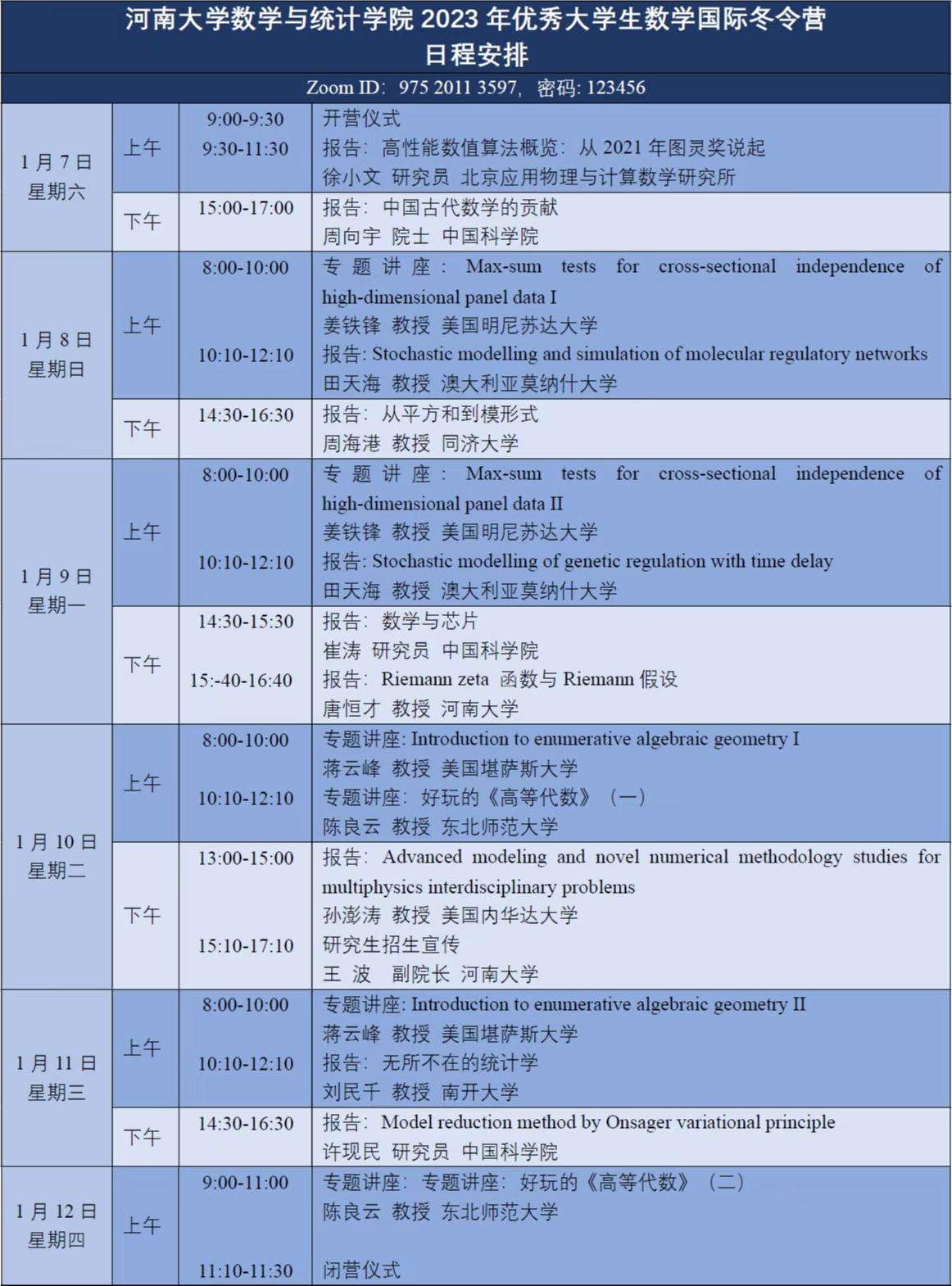
具体日程安排:
讲座题目与摘要
报告人:徐小文 研究员
题 目: 高性能数值算法概览:从2021年图灵奖说起
摘 要: 2022年3月30日,ACM宣布将2021年度图灵奖(A.M.Turing Award)授予美国田纳西大学计算科学家Jack Dongarra教授,以表彰他在数值算法和高性能算法库方面的开创性贡献、其使得高性能计算软件在过去40多年能够跟上超级计算机硬件算力的指数级发展速度。这是图灵奖颁奖五十多年以来,首次颁给超级计算领域。本报告从今年的图灵奖谈起,带领大家走进国之重器超级计算机的日常,通过实际案例展示超级计算的广泛应用,重点介绍高性能数值算法对超级计算的重要作用。
报告人:周向宇 院士
题 目: 中国古代数学的贡献
摘 要: 中国古代数学“言约旨远”。透过其“言约”,揭示其“旨远”,本讲包括:
1、复原商高对勾股定理的完整证明,从而表明正是商高开启命题证明之先河;
2、发现花拉子米代数学思想均含于中国古代数学思想之中,从而解决阿拉伯代数的思想源泉问题;
3、揭示中国古算与国学的联系、诸子百家核心人文思想与数学思想的融合、古算对语言的影响;
4、发现国学经典中的数学,包括《愚公移山》蕴藏的数学思想。
报告人:姜铁锋 教授
题 目: Max-sum tests for cross-sectional independence of high-dimensional panel data
摘 要: We consider a testing problem for cross-sectional independence for high-dimensional panel data, where the number of cross-sectional units is potentially much larger than the number of observations. The cross-sectional independence is described through linear regression models. We study three tests named the sum, the max and the max-sum tests, where the latter two are new. The sum test is initially proposed by Breusch and Pagan (1980). We design the max and sum tests for sparse and nonsparse correlation coefficients of random errors between the linear regression models, respectively. And the max-sum test is devised to compromise both situations on the correlation coefficients. Indeed, our simulation shows that the max-sum test outperforms the previous two tests. This makes the max-sum test very useful in practice where sparsity or not for a set of numbers is usually vague. Toward the theoretical analysis of the three tests, we have settled two conjectures regarding the sum of squares of sample correlation coefficients asked by Pesaran (2004 and 2008). In addition, we establish the asymptotic theory for maxima of sample correlation coefficients appeared in the linear regression model for panel data, which is also the first successful attempt to our knowledge. To study the max-sum test, we create a novel method to show asymptotic independence between maxima and sums of dependent random variables. We expect the method itself is useful for other problems of this nature. Finally, an extensive simulation study as well as a case study are carried out. They demonstrate advantages of our proposed methods in terms of both empirical powers and robustness for correlation coefficients of residuals regardless of sparsity or not.
报告人:田天海 教授
题 目一: Stochastic modelling and simulation of molecular regulatory networks
摘 要: Biological experimental studies have shown that gene expression is a stochastic process. In recent years stochastic models have been developed to investigate the functions of noise in a wide range of biological systems. We will discuss stochastic simulation algorithm for modelling genetic regulations due to the small copy numbers inside the cell. In addition, we will discuss the tau-leap methods for reducing the large computing time required for stochastic simulation algorithm.
题 目二: Stochastic modelling of genetic regulation with time delay
摘 要: Gene expression is a process involving multi-step reactions. To describe such multi-step reactions with accuracy, chemical reactions with time delay have been used in the modelling of genetic regulation. We will discuss the delayed stochastic simulation algorithm (DSSA) and more efficient simulation algorithms for chemical reaction systems with time delay.
报告人:周海港 教授
题 目: 从平方和到模形式
摘 要: 平方和问题是数论中最经典的问题之一,随着数学其它分支的发展,不断有新的工具用于研究这个问题,而模形式理论给出平方和问题一个更优美、更深刻的解决方法。模形式理论融合了代数、几何、分析和数论等众多数学分支成为朗兰兹纲领的核心,在很多领域都有重要而深刻的应用。本讲座从平方和问题出发,简要介绍模形式理论的性质与应用。
报告人:崔涛 研究员
题 目: 数学与芯片
摘 要: 芯片是现代人生活中不可或缺的工业产品。从上个世纪50年代末第一块集成电路诞生至今,工程师们已经可以做到把数亿个晶体管放到一个平方毫米区域上。将沙子变成芯片需要经过一系列复杂的设计和制造过程。本报告将通过具体实例讲述数学是如何在芯片设计与制造过程中发挥重要作用。
报告人:唐恒才 教授
题 目: Riemann zeta 函数与Riemann假设
摘 要: 本报告主要分为两个部分。第一,从数学分析出发,简单介绍Riemann zeta 函数及其解析性质。第二,从非零区域、零点密度、亚凸性估计、临界线上的零点分布这四个视角探讨Riemann猜想的最新研究进展。
报告人:蒋云峰 教授
题 目: Introduction to enumerative algebraic geometry
摘 要: Modern enumerative algebraic geometry is a broad and important branch in Geometry which has close relation and impact on theoretical physics such as string theory, Yang-Mills gauge theory and quantum field theory. We will introduce the basic idea of enumerative geometry from interesting examples. Our main focus is the Gromov-Witten invariants, which are counting invariants via moduli space of stable maps. We will introduce the idea of moduli space in interesting examples.
报告人:陈良云 教授
题 目: 好玩的《高等代数》
摘 要: 将把《高等代数》的行列式、矩阵、多项式和线性空间理论等理论,应用到初等数学、数论、数学分析、李代数等,讲座将涉及一些最新成果与前沿问题。
报告人:孙澎涛 教授
题 目:Advanced modeling and novel numerical methodology studies for multiphysics interdisciplinary problems
摘 要:My talk will center around advanced modeling and novel numerical methodology studies for multiphysics problems arising from the state-of-art, interdisciplinary, real-world applications, which include but not limited to (1) proton exchange membrane fuel cell (PEMFC) dynamics; (2) fluid-structure interactions (FSI) problems. All real-world problems may possess sophisticated features of multiphysics, multidimensionality, multi-component, multiphase, anisotropy, nonlinearity and etc. Without loss of generality in this talk, based upon the above two types of multiphysics problems, I will focus on how to utilize partial differential equations (PDEs) to model real-world problems, and how to numerically solve the derived PDEs for the solution of targeted problems.
From my talk, senior undergraduate students may learn how mathematics can finally manufacture productivity for human society, and how mathematics can impact developments of interdisciplinary subjects; graduate students can learn more about how to apply fundamental mathematics to real-world problems that cannot be solved analytically, and conversely, how engineering applications and experimental studies can promote the development of modern applied mathematics.
Audiences who are not interested in more details about my talk may skip the following paragraph. Whereas, considering this is still an academic presentation, below I would rather like to demonstrate some technical details about my talk, just for the interested audiences’ information. Particularly, two types of real-world problems and their novel numerical methodology studies will be addressed in my talk, as shown below.
1.A multiphase mixture formulation defined in a single computational domain will be presented to model the fluid flow in PEMFC. A type of combined finite element-upwind finite volume method combining with Newton's linearization, streamline-diffusion scheme, Galerkin-least square scheme and other numerical techniques such as Kirchhoff transformation is illustrated for achieving an overall fast and stable convergent numerical simulation, where, flow, species, charge-transport and energy equations are discretized and solved in a monolithic and efficient fashion. And, the convergent numerical solutions can be reached within around one hundred steps, comparing to the standard commercial CFD solvers which always produce oscillating iterations and are difficult to reach convergent solutions. A nonlinear Dirichlet/Robin iteration-by-subdomain domain decomposition method will be also demonstrated if multi-layer diffusion media are included in PEMFC to improve liquid-water transport in the porous electrode. For example, assembling of the gas diffusion layer (GDL) and the micro-porous layer (MPL), through the interface of which the capillary pressure is continuous whereas the liquid saturation is discontinuous.
2.The second topic goes to fluid-structure interaction (FSI) problems that describe the interaction of a flexible structure with a flowing fluid in which it is submersed or by which it is surrounded, giving rise to a rich variety of physical phenomena with applications in many fields of engineering and biology. In general, FSI problems require the fluid and the structure fields at the common interface to share not only the same velocity but also the common traction force. There are currently several major approaches classified with respect to the numerical treatment how the interface conditions of FSI are dealt with on the moving interface. In my talk, I will introduce three numerical techniques studied in my research for solving FSI problems: (1) body-fitted mesh (arbitrary Lagrangian-Eulerian) method, (2) body-unfitted mesh (fictitious domain) method, and (3) meshfree (deep neural network) method.
3.Our applications to FSI problems range from hydrodynamics (physics) to hemodynamics (biology, physiology), in which the involved structures are either incompressible or compressible and bear a deformable and/or rotational constitutive relation while the surrounding fluid flow is incompressible or nearly incompressible. For example, the hydro-turbine machine that is widely used in hydropower stations, a rotating artificial heart pump inside the artery to help on curing the heart−failure patients, and an intravascular stent inside the blood fluid to treat the aneurismal patients, finally to improve the human cardiovascular system and to remedy cardiovascular diseases.
报告人:刘民千 教授
题 目: 无所不在的统计学
摘 要: 统计学是收集、整理和分析数据的科学和艺术。统计无所不在,几乎所有的领域都有统计的痕迹。本讲座将带您了解身边的数据、什么是统计学、统计学在各行各业中的应用,以及大数据时代统计学所面临的机遇和挑战。
报告人:许现民 研究员
题 目: Model reduction method by Onsager variational principle
摘 要: The Onsager principle is a fundamental law for irreversible processes in statistic physics. It has been used to develop dynamic models for many problems in soft matter, like the diffusion process, the dynamics of liquid crystal solution and the moving contact line problems, etc. Recently, the variational principle has been used as an approximation tool to derive reduced models for many complicated systems. In this talk, I will present the main idea of the model reduction method based on the Onsager principle. In particular, I will present applications of the method in numerical analysis, including derivation of a diffusion-generated motion method for wetting problems, a moving finite element method for gradient flows and geometric partial differential equations.