为促进高校之间优秀老员工的交流和互动、给员工提供一个了解数学和统计学科各个方向最新前沿动态的机会,mk体育官网拟定于2022年7月11日—7月16日举办老员工数学夏令营(ZOOM视频在线进行)。本次夏令营计划在全国高校范围内招收100名数学、统计学及相关专业的高年级本科生。夏令营期间将通过学术讲座、学院宣讲、导师交流等活动,旨在打造数学和统计学的学习与交流平台,同时展示公司在数学、统计等领域所取得的重要研究成果,使员工了解公司的学科发展特色和公司产品模式。
我们邀请到以下国内外专家为员工讲授专题课、作前沿报告:
纽约大学 杨亦松 教授
美国堪萨斯州立大学 林宗柱 教授
美国迈阿密大学 苗蓬子 教授
澳大利亚莫纳什大学 田天海 教授
北京计算科学研究中心 张智民 教授
浙江大学 李 方 教授
南京邮电大学 王志伟 教授
mk体育 刘张炬 教授
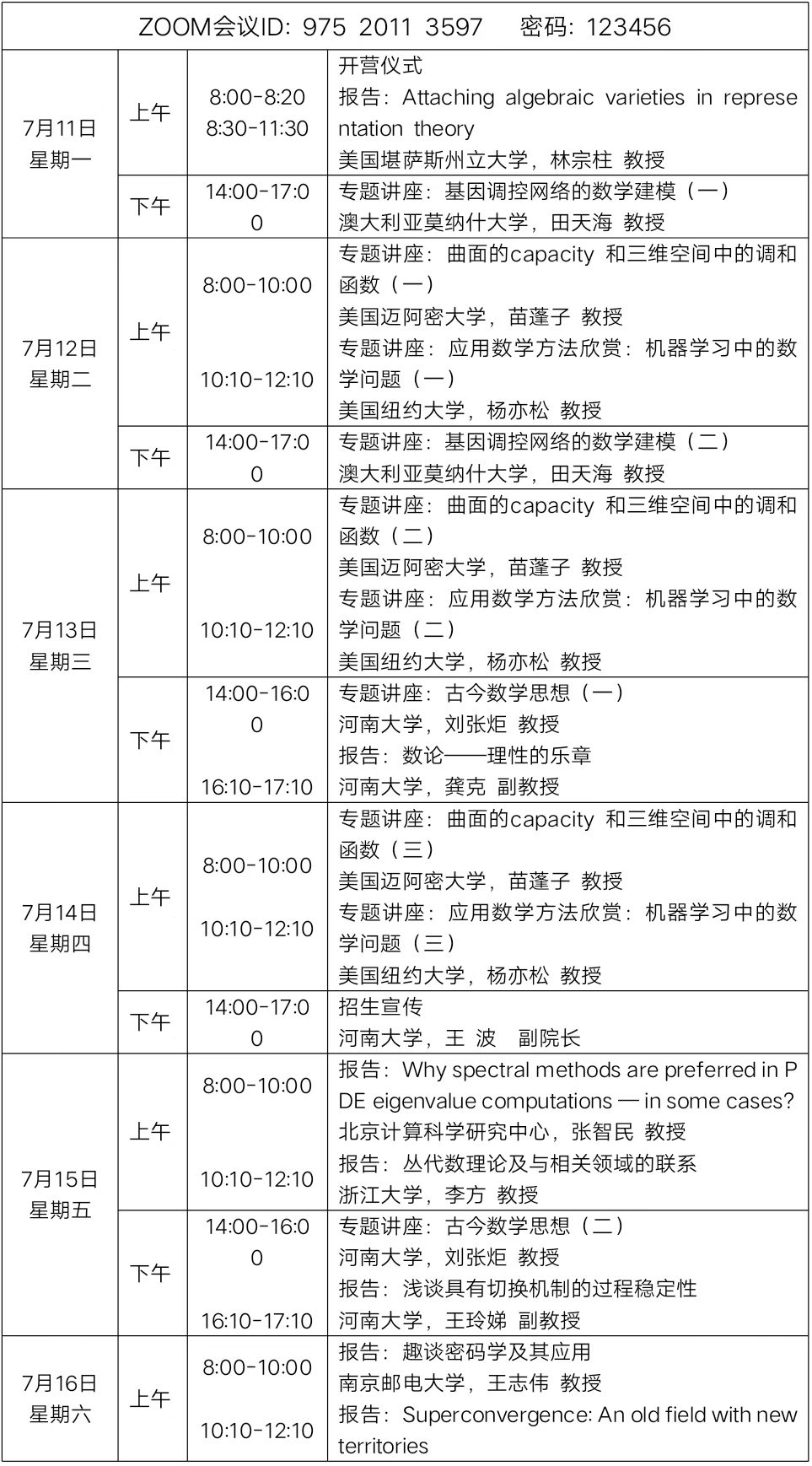
具体日程安排如下:

报告题目、摘要
报告人:林宗柱 教授
题 目:Attaching algebraic varieties in representation theory
摘 要:Given a category of representations of finite groups, Lie algebras, etc, one wants to construct an algebraic variety so that the geometric tools in algebraic variety can be used to study the representation category. There are many ways to do so. One of the ways is to construct an algebraic variety so that representations would corresponds to points in the variety. Another way is to realize representations as sheaves on the algebraic variety. In this talk I will outline a few different constructions to illustrate how geometric tools and representation theory can be closely related. I will take representations of finite froups, or restricted Lie algebras as well as vertex operator algebras as examples. This is also closedly related to non-commutative algebraic geometry.
报告人:苗蓬子 教授
题 目: 曲面的capacity 和三维空间中的调和函数
摘 要: 给定三维欧式空间中的一个闭曲面,除了它自身面积和其包含区域的体积,capacity 是另一个与其相关的几何量。在这个短期课程里,我们讨论一些和capacity 有关的几何不等式。其中很多关于调和函数的使用已经可以反应出最近几年关于三维正质量定理新的证明的想法。
报告人:杨亦松 教授
题 目:应用数学方法欣赏:机器学习中的数学问题
摘 要:作为人工智能领域的一部分,机器学习利用采集到的数据和非预定的程序化方式,用优化的学习方法做出决定或者预测和判断。在这个短课程中,我们将介绍机器学习中的一些基本概念和数学问题。
报告人:田天海 教授
题 目: 基因调控网络的数学建模
摘 要: 基因调控网络是分子生物学中的一个重要和基本的过程。数学建模是描述复杂调控过程的一个重要工具。本系列讲座将介绍基因调控的一些基本生物概念和基于微分方程的动态建模方法。第一部分:生物概念和建模技巧。这部分将介绍基因调控的一些基本生物概念和建模技巧,包括网络的图形表示,正向调控和逆向调控。同时也讨论模型的一些重要性质,包括模型的鲁棒性和敏感性。第二部分:基因调控模型的例子。本部分将利用三个模型来讨论基因调控的重要性质。这三个模型是经典的λ噬菌体模型(正向和逆向调控),遗传拨动开关(双稳性质)和血液干细胞(三稳性质)。第三部分:基于组学数据的网络推断。本部分将讨论如何利用组学数据来构建基因调控网络。我将讨论利用相关性的方法来构建静态调控网络和利用数学模型方法来构建动态网络。第四部分:模型未知参数估计的贝叶斯方法。本部分将介绍用于估计基因网络模型中未知参数的贝叶斯方法。本部分将介绍用于估计基因网络模型中未知参数的贝叶斯方法。我们将讨论衡量参数样本好坏的测度以及近年来被广泛使用的近似贝叶斯计算方法。
报告人:张智民 教授
题 目1: Why spectral methods are preferred in PDE eigenvalue computations ---in some cases?
摘 要: When approximating PDE eigenvalue problems by numerical methods such as finite difference and finite element, it is common knowledge that only a small portion of numerical eigenvalues are reliable. As a comparison, spectral methods may perform extremely well in some situation, especially for 1-D problems. In addition, we demonstrate that spectral methods can outperform traditional methods and the state-of-the-art method in 2-D problems even with singularities.
题 目2:Superconvergence: An Old Field with New Territories
摘 要:Superconvergence phenomenon is well understood for the h-version finite element method and researchers in this old field have accumulated a vast literature during the past 50 years. However, the relevant study for other numerical methods such as the p-version finite element method, spectral methods, discontinuous Galerkin methods, and finite volume methods is lacking. We believe that the scientific community would also benefit from the study of superconvergence phenomenon of those methods. Some efforts have been made to expand the territory of the superconvergence. In this talk, we present some recent development on superconvergence study for the spectral collocation methods, discontinuous Galerkin methods, and finite volume methods. At the same time, some current issues and un-solved problems will also be addressed.
报告人:李方 教授
题 目: 丛代数理论及与相关领域的联系
摘 要: 本报告将介绍丛代数的定义、基本性质、与代数表示论、拓扑学以及数论等的基本联系。
报告人: 王志伟 教授
题 目:趣谈密码学及其应用
摘 要:密码学是研究保密通信的一门科学。它研究在不安全的环境中,如何把所要传输的信息在发给接收者之前进行秘密转换以防止第三者对信息的窃取。密码学具有很强的实践性,有许多当今非常流行应用场景,同时也具有很强的理论性,与代数数论等有密切的关系。报告主要内容包括:密码学的前世、今生和未来;密码学的地位和作用;密码算法的分类及其与数学的关系;密码学的若干应用场景等。
报告人:刘张炬 教授
题 目: 古今数学思想
摘 要: 本课程以几何学的发展为线索,简要介绍从古至今人类取得的重大数学成就以及其中蕴含的核心思想,同时指出杰出人物在推动数学发展的进程中起到了决定性作用。
报告人:龚克 副教授
题 目:数论——理性的乐章
摘 要:数论亦称高等算术,因其真其美而行之久远。通过撷取著名的历史片段,展示数论研究的特点与思想方法,并介绍相关的前沿问题。
报告人:郑晨 副教授
题 目:统计学:推开时代的大门,发现数据的秘密
摘 要:统计学(Statistics)是一门利用数据探索自然规律的科学,随着大数据时代的来临,统计学得以迅猛发展,在人工智能、经济、金融等领域都发挥了重要的作用。本讲座将介绍统计学的基本面貌、一些统计学的精彩案例和应用研究,希望能激发大家对统计学的研究兴趣。
报告人:王玲娣 副教授
题 目: 浅谈具有切换机制的过程稳定性
摘 要: 作为概率论与数理统计中的一个研究方向,随机切换加上随机过程构成的混悬系统具有自身的特点和魅力,该类模型在多个学科领域有重要应用。通过介绍该模型及其稳定性,了解该类过程的一些前沿知识。